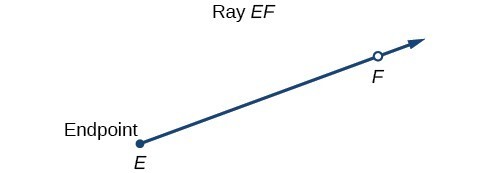
Figure 1
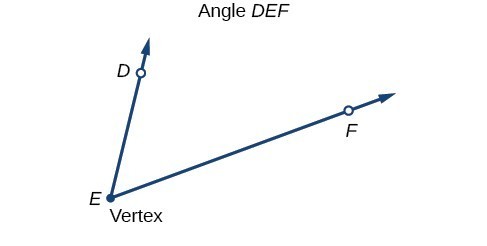
Figure 2
| theta | phi | alpha | beta | gamma |
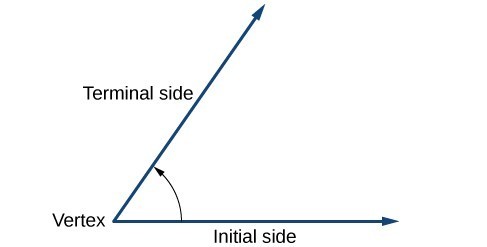
Figure 4
Converting Between Degrees and Radians
Dividing a circle into 360 parts is an arbitrary choice, although it creates the familiar degree measurement. We may choose other ways to divide a circle. To find another unit, think of the process of drawing a circle. Imagine that you stop before the circle is completed. The portion that you drew is referred to as an arc. An arc may be a portion of a full circle, a full circle, or more than a full circle, represented by more than one full rotation. The length of the arc around an entire circle is called the circumference of that circle. The circumference of a circle is . If we divide both sides of this equation by , we create the ratio of the circumference to the radius, which is always regardless of the length of the radius. So the circumference of any circle is times the length of the radius. That means that if we took a string as long as the radius and used it to measure consecutive lengths around the circumference, there would be room for six full string-lengths and a little more than a quarter of a seventh, as shown in Figure 10.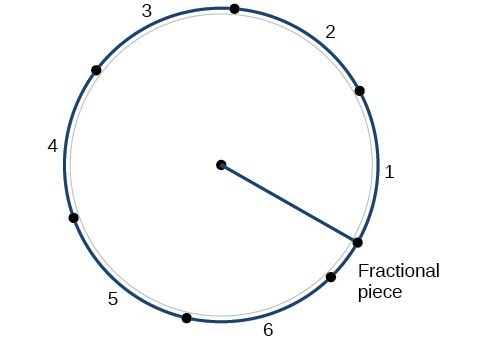
Figure 10
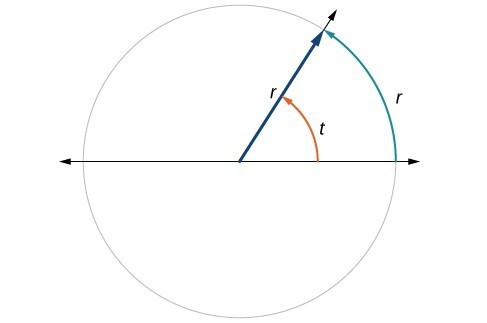
Figure 11. The angle t sweeps out a measure of one radian. Note that the length of the intercepted arc is the same as the length of the radius of the circle.
Relating Arc Lengths to Radius
An arc length is the length of the curve along the arc. Just as the full circumference of a circle always has a constant ratio to the radius, the arc length produced by any given angle also has a constant relation to the radius, regardless of the length of the radius. This ratio, called the radian measure, is the same regardless of the radius of the circle—it depends only on the angle. This property allows us to define a measure of any angle as the ratio of the arc length to the radius .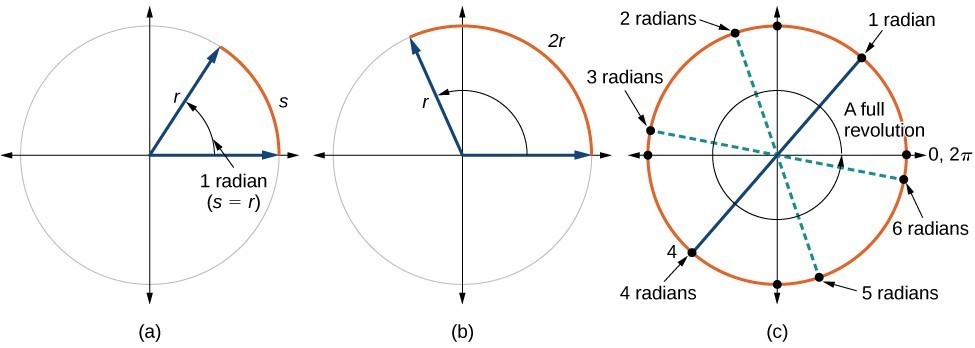 Figure 12. (a) In an angle of 1 radian, the arc length
equals the radius
. (b) An angle of 2 radians has an arc length
. (c) A full revolution is
or about 6.28 radians.
To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is
, where
is the radius. The smaller circle then has circumference
and the larger has circumference
. Now we draw a 45° angle on the two circles, as in Figure 13.
Figure 12. (a) In an angle of 1 radian, the arc length
equals the radius
. (b) An angle of 2 radians has an arc length
. (c) A full revolution is
or about 6.28 radians.
To elaborate on this idea, consider two circles, one with radius 2 and the other with radius 3. Recall the circumference of a circle is
, where
is the radius. The smaller circle then has circumference
and the larger has circumference
. Now we draw a 45° angle on the two circles, as in Figure 13.
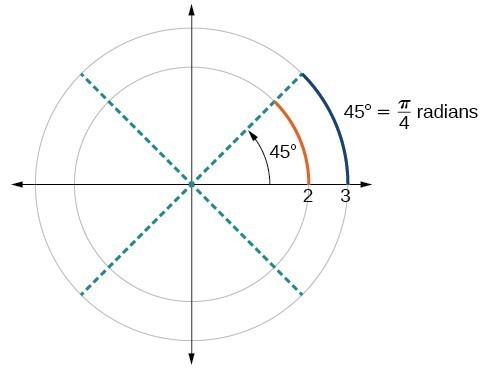
Figure 13. A 45° angle contains one-eighth of the circumference of a circle, regardless of the radius.
A GENERAL NOTE: RADIANS
One radian is the measure of the central angle of a circle such that the length of the arc between the initial side and the terminal side is equal to the radius of the circle. A full revolution (360°) equals radians. A half revolution (180°) is equivalent to radians. The radian measure of an angle is the ratio of the length of the arc subtended by the angle to the radius of the circle. In other words, if is the length of an arc of a circle, and is the radius of the circle, then the central angle containing that arc measures radians. In a circle of radius 1, the radian measure corresponds to the length of the arc.
Q & A
A MEASURE OF 1 RADIAN LOOKS TO BE ABOUT 60°. IS THAT CORRECT?
Yes. It is approximately 57.3°. Because radians equals 360°, radian equals .Using Radians
Because radian measure is the ratio of two lengths, it is a unitless measure. For example, in Figure 12, suppose the radius were 2 inches and the distance along the arc were also 2 inches. When we calculate the radian measure of the angle, the “inches” cancel, and we have a result without units. Therefore, it is not necessary to write the label “radians” after a radian measure, and if we see an angle that is not labeled with “degrees” or the degree symbol, we can assume that it is a radian measure. Considering the most basic case, the unit circle (a circle with radius 1), we know that 1 rotation equals 360 degrees, 360°. We can also track one rotation around a circle by finding the circumference, , and for the unit circle . These two different ways to rotate around a circle give us a way to convert from degrees to radians.Identifying Special Angles Measured in Radians
In addition to knowing the measurements in degrees and radians of a quarter revolution, a half revolution, and a full revolution, there are other frequently encountered angles in one revolution of a circle with which we should be familiar. It is common to encounter multiples of 30, 45, 60, and 90 degrees. These values are shown in Figure 14. Memorizing these angles will be very useful as we study the properties associated with angles.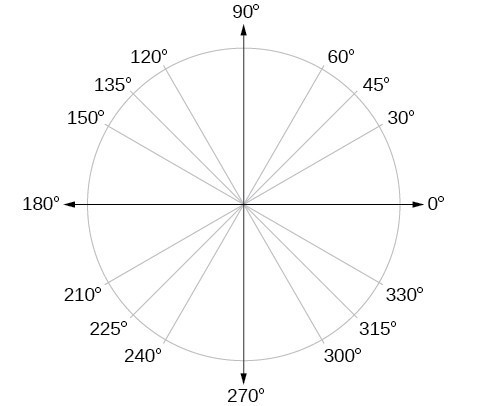
Figure 14. Commonly encountered angles measured in degrees
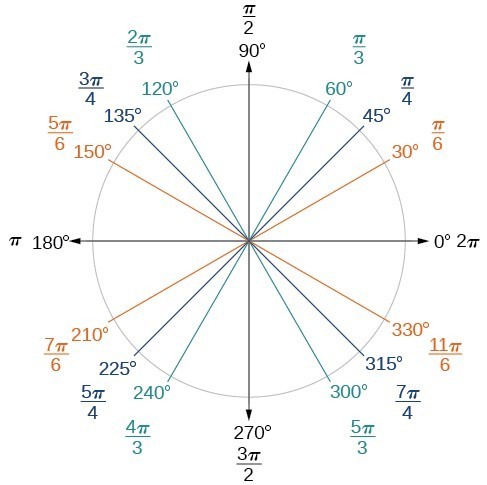
Figure 15. Commonly encountered angles measured in radians
EXAMPLE 2: FINDING A RADIAN MEASURE
Find the radian measure of one-third of a full rotation.SOLUTION
For any circle, the arc length along such a rotation would be one-third of the circumference. We know thatTRY IT 2
Find the radian measure of three-fourths of a full rotation. SolutionConverting between Radians and Degrees
Because degrees and radians both measure angles, we need to be able to convert between them. We can easily do so using a proportion.Converting between Radians and Degrees
To convert between degrees and radians, use the proportionEXAMPLE 3: CONVERTING RADIANS TO DEGREES
Convert each radian measure to degrees. a. b. 3SOLUTION
Because we are given radians and we want degrees, we should set up a proportion and solve it. a. We use the proportion, substituting the given information.TRY IT 3
Convert radians to degrees. SolutionEXAMPLE 4: CONVERTING DEGREES TO RADIANS
Convert degrees to radians.SOLUTION
In this example, we start with degrees and want radians, so we again set up a proportion and solve it, but we substitute the given information into a different part of the proportion.Analysis of the Solution
Another way to think about this problem is by remembering that . Because , we can find that is .TRY IT 4
Convert 126° to radians. SolutionWatch the following video for an explanation of radian measure and examples of converting between radians and degrees.
Any angle has infinitely many coterminal angles because each time we add 360° to that angle—or subtract 360° from it—the resulting value has a terminal side in the same location. For example, 100° and 460° are coterminal for this reason, as is −260°. Recognizing that any angle has infinitely many coterminal angles explains the repetitive shape in the graphs of trigonometric functions.
An angle’s reference angle is the measure of the smallest, positive, acute angle
formed by the terminal side of the angle
and the horizontal axis. Thus positive reference angles have terminal sides that lie in the first quadrant and can be used as models for angles in other quadrants. See Figure 17 for examples of reference angles for angles in different quadrants.
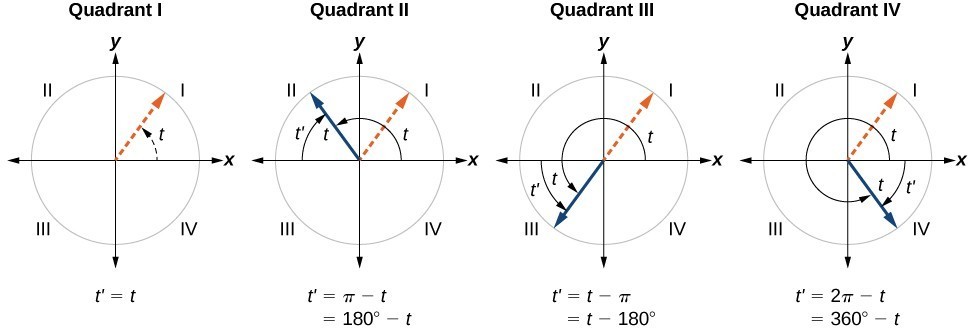
Figure 17
A GENERAL NOTE: COTERMINAL AND REFERENCE ANGLES
Coterminal angles are two angles in standard position that have the same terminal side. An angle’s reference angle is the size of the smallest acute angle, , formed by the terminal side of the angle and the horizontal axis.HOW TO: GIVEN AN ANGLE GREATER THAN 360°, FIND A COTERMINAL ANGLE BETWEEN 0° AND 360°.
- Subtract 360° from the given angle.
- If the result is still greater than 360°, subtract 360° again till the result is between 0° and 360°.
- The resulting angle is coterminal with the original angle.
EXAMPLE 5: FINDING AN ANGLE COTERMINAL WITH AN ANGLE OF MEASURE GREATER THAN 360°
Find the least positive angle that is coterminal with an angle measuring 800°, where .SOLUTION
An angle with measure 800° is coterminal with an angle with measure 800 − 360 = 440°, but 440° is still greater than 360°, so we subtract 360° again to find another coterminal angle: 440 − 360 = 80°. The angle is coterminal with 800°. To put it another way, 800° equals 80° plus two full rotations, as shown in Figure 18.
Figure 18
TRY IT 5
Find an angle that is coterminal with an angle measuring 870°, where . SolutionHOW TO: GIVEN AN ANGLE WITH MEASURE LESS THAN 0°, FIND A COTERMINAL ANGLE HAVING A MEASURE BETWEEN 0° AND 360°.
- Add 360° to the given angle.
- If the result is still less than 0°, add 360° again until the result is between 0° and 360°.
- The resulting angle is coterminal with the original angle.
EXAMPLE 6: FINDING AN ANGLE COTERMINAL WITH AN ANGLE MEASURING LESS THAN 0°
Show the angle with measure −45° on a circle and find a positive coterminal angle such that 0° ≤ α < 360°.SOLUTION
Since 45° is half of 90°, we can start at the positive horizontal axis and measure clockwise half of a 90° angle. Because we can find coterminal angles by adding or subtracting a full rotation of 360°, we can find a positive coterminal angle here by adding 360°:
Figure 19
Watch this video for another example of how to determine positive and negative coterminal angles.
TRY IT 6
Find an angle that is coterminal with an angle measuring −300° such that . SolutionFinding Coterminal Angles Measured in Radians
We can find coterminal angles measured in radians in much the same way as we have found them using degrees. In both cases, we find coterminal angles by adding or subtracting one or more full rotations.
Given an angle greater than
, find a coterminal angle between 0 and
.
- Subtract from the given angle.
- If the result is still greater than , subtract again until the result is between and .
- The resulting angle is coterminal with the original angle.
EXAMPLE 7: FINDING COTERMINAL ANGLES USING RADIANS
Find an angle that is coterminal with , where .SOLUTION
When working in degrees, we found coterminal angles by adding or subtracting 360 degrees, a full rotation. Likewise, in radians, we can find coterminal angles by adding or subtracting full rotations of radians: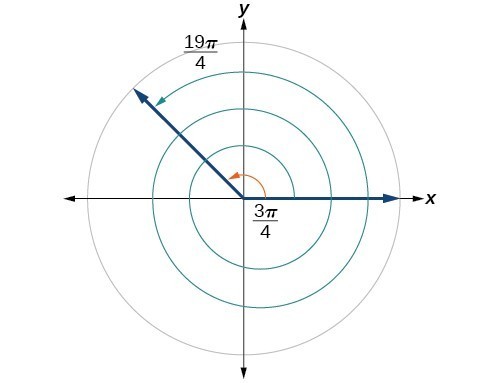
Figure 20
 Figure 20
Figure 20 Figure 21. The area of the sector equals half the square of the radius times the central angle measured in radians.
Figure 21. The area of the sector equals half the square of the radius times the central angle measured in radians. Figure 22. The sprinkler sprays 20 ft within an arc of 30°.
Figure 22. The sprinkler sprays 20 ft within an arc of 30°. Figure 23
Figure 23 Figure 24
Figure 24 Figure 25
Figure 25